Doğada Fibonacci

İtalyan bir tüccar olan Fibonacci (1170–1240), aynı zamanda parlak bir matematikçi olduğu için Avrupa’da ünlü oldu. En büyük başarılarından biri, Roma rakamlarının yerine Arap rakamlarını tanıtmasıydı.

Aşağıdaki gibi çalışan Fibonacci Toplama Serisini geliştirdi:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .

Matematiksel seri, sabit bir orana doğru asimptotik olarak (giderek daha yavaş yaklaşır) eğilim gösterir.

Ancak bu irrasyonel bir orandır; kendisinden sonra gelen, asla bitmeyen, tahmin edilemeyen bir ondalık değer dizisi vardır ve asla tam olarak ifade edilemez. Serinin parçası olan her sayı, kendinden önceki değere bölünürse (örneğin, 13  8 veya 21  13), işlem 1.61803398875 . . . irrasyonel rakamı etrafında salınan, bir zaman orandan daha yüksek, bir sonraki zaman daha düşük olan bir oranla sonuçlanır. Kesin oranı sonsuza kadar asla bilemeyeceğiz (çağımızın güçlü bilgisayarlarıyla bile). Kısa tutmak adına Fibonacci oranından 1,618 olarak bahsediyoruz ve okuyucudan hata payını aklında tutmasını istiyoruz.

Bu oran, başka bir ortaçağ matematikçisi olan Luca Pacioli (1445–1514) ona “ilahi oran” demeden önce bile özel isimler toplamaya başlamıştı. Çağdaş isimleri arasında “altın oran” ve “altın ortalama” vardır. Alman bir astronom olan Johannes Kepler (1571–1630), Fibonacci oranından geometrideki mücevherlerden biri olarak bahsetmiştir. Cebirsel olarak, genellikle Yunan harfi PHI ile gösterilir:

PHI  1.618

Ve bilim insanları (ve tüccarlar) için ilginç olan sadece PHI değildir. Fibonacci toplama serisinin herhangi bir sayısını onu takip eden sayıya bölersek (örneğin, 8  13 veya 13  21), seri asimptotik olarak PHI  oranına yaklaşır .

PHI   0,618

Bu dikkat çekici bir olgudur ve işlem araçları tasarlarken kullanışlıdır. Orijinal PHI oranı irrasyonel olduğundan, PHI oranına karşılık gelen PHI  değeri de zorunlu olarak irrasyonel bir rakamdır, bu da yaklaşık, kısaltılmış bir şekilde 0,618 hesaplanırken yine hafif bir hata payı olduğu anlamına gelir.

Fibonacci ile bilime uygulanabilecek bir dizi düz sayı keşfettik. Fibonacci toplama serisini ticaret araçları geliştirmek için kullanmaya çalışmadan önce, doğadaki ilişkisini göz önünde bulundurmak faydalı olacaktır. O zaman, hakkında sonuçlara ulaşmak için sadece küçük bir adımdır

Fibonacci toplamının uluslararası piyasa hareketlerindeki önemi, ister para birimleri, ister emtialar, ister hisse senetleri veya türevler olsun. İnsanlar bilinçaltında, rahat bir yaşam standardı yaratmak için sürekli ve zamansız bir çabadan başka bir şey olmayan ilahi oranı ararlar.

Doğa ve Geometride Fibonacci Toplama Serisi

Fibonacci dizisi kullanılarak ne kadar çok sabit değerin hesaplanabildiği ve dizideki bireysel sayıların ne kadar çok çeşitlilikte tekrarlandığı dikkat çekicidir.

Ancak bu sadece bir sayı oyunu değil; şimdiye kadar keşfedilmiş en önemli doğal fenomen matematiksel temsilidir. Genel olarak konuşursak, Fibonacci toplam serisi doğanın yasasıdır ve herhangi bir mükemmel şekil veya eğride bulunan estetiğin bir parçasıdır.

Fibonacci, tek bir tavşan çiftinin yavrularının tekrarlanabilir bir düzende arttığını öne sürdüğünde, doğa yasasının toplama serileriyle nasıl ilişkili olduğunu keşfetti:

Ocak ayında bir çift tavşan olduğunu ve ardından Şubat ayında ikinci bir çift tavşan ürettiğini ve bundan sonra bu yavruların her ay başka bir çift ürettiğini varsayalım. Matematiksel problem, Aralık ayının sonunda kaç çift tavşan olacağını bulmaktır.

Bu küçük cebirsel bulmacayı çözmek için verileri dört sütuna ayıracağız:

1. Her ayın başındaki toplam üreme tavşanı çifti sayısı.
2. Her ayın başında üremeyen tavşan çiftlerinin toplam sayısı.
3. Her ay üreyen tavşan çiftlerinin toplam sayısı.
4. 12 ayın sonunda üreyen toplam tavşan çifti sayısı.

Tablo 3.1, dört kritere göre toplam tavşan sayısına doğru ilerlemeyi göstermektedir.

Tablo 3.1 Tek Bir Tavşan Çiftinin Yavruları

Her sütun, herhangi bir sayının kendisinden hemen önce gelen sayı çiftlerinin toplamına eşit olduğu kuralına göre oluşturulmuş Fibonacci toplam serisini içerir.

Fibonacci oranının (PHI) doğal bir sabit olarak önemini takdir etmek için doğanın güzelliğine bakmak yeterlidir. Birçok büyüyen bitkinin gövdelerindeki koltuk altı sayısı ve alçalan bitkilerdeki taç yapraklarının sayısı, Fibonacci oranı ve altta yatan toplama serilerinin birçok örneğini sunar. Aşağıdaki çizimler bu matematiksel dizinin bazı ilginç uygulamalarını tasvir eder.

Bitkilerde Bulunan Fibonacci Sayıları

Avrasya’ya özgü bir bitki olan hapşırıkotu, doğadaki Fibonacci toplama serisinin ideal bir örneğidir; zira her yeni dal koltuk altından çıkar ve yeni bir daldan da başka dallar büyür.

Eski ve yeni dalların birlikte eklenmesi, her yatay düzlemde Fibonacci toplam serisinin sayısını ortaya çıkarır. Şekil 3.1 sayımı göstermektedir.

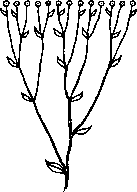
Şekil 3.1 Hapşırıkotu çiçeklerinde bulunan Fibonacci sayıları. 

Aynı cebirsel ilkeye göre, bitki yaşamındaki Fibonacci toplam serisini (altın sayılar olarak adlandırılır) belirli yaygın çiçeklerin taç yapraklarını sayarak kolayca belirleyebiliriz. 3 taç yapraklı iris, 5 taç yapraklı çuha çiçeği, 13 taç yapraklı ragwort, 34 taç yapraklı papatya ve 55 (ve 89) taç yapraklı michalmas papatyası ele alındığında, bu desenin tesadüfi mi yoksa belirli bir doğa yasası mı olduğu sorgulanmalıdır.

Ayçiçeğinde Dönüşüm Kuralı

Ayçiçeğinin güzel kıvrımlı çizgileri binlerce yüzyıldır doğada var olmuştur ve matematikçiler bunları yüzlerce yıldır araştırma konusu yapmışlardır.

Ayçiçeği, biri saat yönünde, diğeri saat yönünün tersine dönen, üst üste bindirilmiş ve iç içe geçmiş iki eş açılı spiral kümesine sahiptir. 21 saat yönünde ve 34 saat yönünün tersine spiral vardır. Her iki sayı da Fibonacci toplama serisinin bir parçasıdır. Sıra, Elliott’un insan davranışını açıklamak için dalga prensiplerinde kullandığı dönüşüm kuralıyla yakından ilişkilidir (bkz. Şekil 3.2).

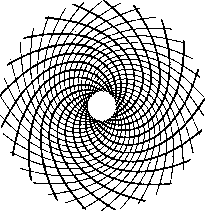
Şekil 3.2 Ayçiçeğinde gösterilen dönüşüm kuralı. 

Altın Dikdörtgen ve Altın Kesitin Geometrisi

Ünlü Yunan matematikçi Megaralı Öklid ( M.Ö. 450-370 ) , altın oran hakkında yazan ve doğrunun analizine odaklanan ilk bilim insanıydı.

Altın dikdörtgenin geometrisinin daha karmaşık yapısı Şekil 3.3’te gösterilmiştir. Dikdörtgenin uzun kenarının kısa kenarına oranı Fibonacci oranı olarak 1,618’dir.

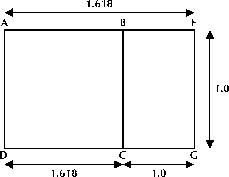
Şekil 3.3 Altın dikdörtgenin geometrisi.

Atina’daki Parthenon Tapınağı

Atina’daki Parthenon Tapınağı’nın oranları, altın dikdörtgenin yanı sıra altın oranın Yunan mimarisindeki etkisini de kanıtlıyor.

Parthenon tapınağının oranları tam olarak altın bir dikdörtgene uymaktadır; toplam genişliği yüksekliğinin tam 1,618 katıdır (bkz. Şekil 3.4).

Şekil 3.4 Atina’daki Parthenon tapınağı.

İnsanlık için önemli olan diğer geometrik eğriler doğada bol miktarda bulunur. Uygarlık için en önemli olanlar arasında okyanus ufku, meteor izi, şelalenin parabolü, güneşin gökyüzünde kat ettiği yay, hilal ve bir kuşun uçuşu yer alır.

Bu doğal eğrilerin çoğu elipsler kullanılarak geometrik olarak modellenebilir. İkinci bulgu, Fibonacci oranını kullanan işlem araçlarının kısa bir açıklamasına yol açar. Bu araçların yapısı ve işlevleri hakkında temel bir bilgi, bu kitapta daha sonra tanıtılacak işlem stratejilerini anlamak için gereklidir.